[모두의연구소][K-디지털서포터즈] Diffusion 관련 논문 리뷰 1

 

 

 

안녕하세요 늑대양입니다 😍

 

 

이번에 모두의연구소에서 K-디지털 서포터즈로 선정되어 금일부터 12월 23일까지 활동하게 되었습니다.

 

 

오늘은 관련 활동의 세 번째 포스팅으로 모두의연구소 MODUPOP에 참석한 경험을 공유드리고자 합니다.

 

 

 

 

생성모델부터 Diffusion 까지 - 4회차 - diffusion 관련 논문 리뷰 1

 

 

 

컨퍼런스 장 내부 모습!!

 

 

 

Diffusion 관련 논문 리뷰 1

• 이상윤 님 진행

 

 

Introduction

Diffusion models

• Diffusion probabilitstic models
• Score-based models

 

• DPMs: natural connection with variational approaches
• SBMs: closely related to EBMs (learning an unnormalized density
• Both perspectives are useful for understanding the recently rising iterative methods

 

 

Generative modeling

How to construct a flexible pdf?

• Invertible flows - lack of flexibility
• VAEs - surrogate loss
• AR models - sampling speed
• GANs (learning implicit models with min-max game) - training instability

 

 

Energy-based models

• Gibbs distribution
• Partition function
• Maximum likelihood training

 

 

Score matching

• Due to the intractable partition function, maximum likelihood training is slow.
• Instead, parameterize the log derivative of the density (i.e., score function)
  • The partition function disappears as it is not a function of data
• Then, generative modeling is turned into a simple regression task
• Yet, Jacobian trace of the score network is expensive to compute
• 이미지 기준 dimension: 300만

 

 

Denoising score matching

• Score matching in the noised data distribution is easier.
• For a Gaussian perturbation kernel
• The above objective is reduced to, which is equivalent to the objective of denoising autoencoders.
• However, we cannot learn the score of the true data distribution

 

 

Sampling with Langevin MCMC

• Given a score function, we can sample using Langevin MCMC:
• But there are pitfalls...

 

 

Pitfall 1: Inaccurate score estimation in the low-density regions

• The manifold hypothesis tells us that data lies in the low-dimensional manifold.
• As we sample from data distribution, the learned score is accurate only at the data manifold.
• This is problematic as we usually initialize the MCMC with noises.

 

 

Pitfall 2: Relative weights

Relative weights

 

 

 

Learning multi-scale score network

• Generative Modeling by Estimating Gradients of the Data Distribution
• Adding Gaussian noise to data can be viewed as "blurring" the data distribution.
• But how to determine the noise strength? >> gradually decrease the variance.

 

 

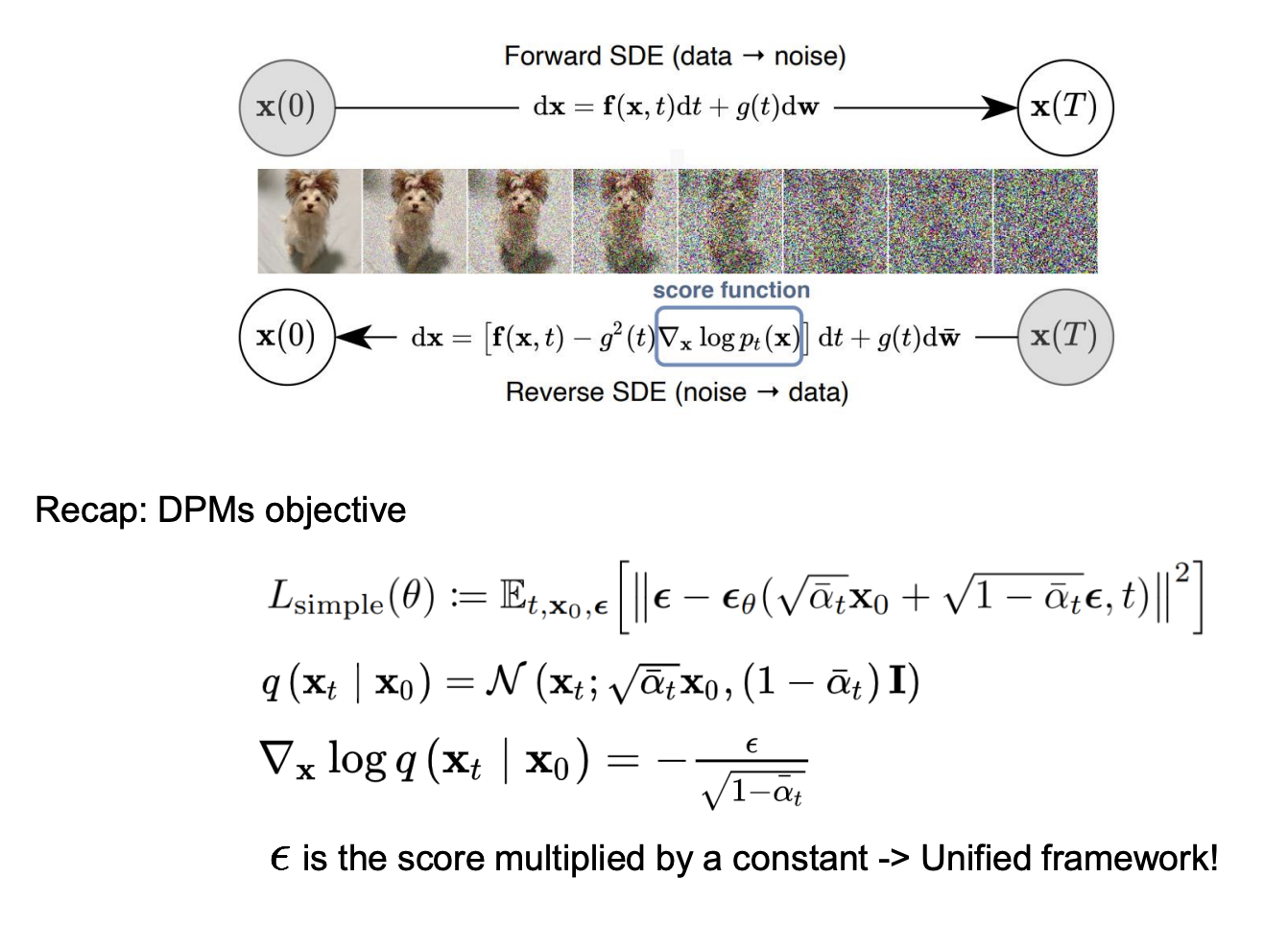
Connection with stochastic differential equations

• A generalizaed framework that unifies the DPMs and SBMs.
• Reveals connection with continuous-time normalizing flows.
• Controllable generation thanks to the modularity of the score networks.

 

 

Stochastic differntial equations

• Anderson(1982): A reverse of the diffusion process is also a diffusion process, running backwards in time and given by the reverse-time SDE:
• Can be estimated by learning time conditional score network

 

 

DPMs and SBMs are the SDEs

DPMs and SBMs are the SDEs - 1

 

 

 

DPMs and SBMs are the SDEs - 2

 

 

 

Probability flow ODE

• Generative SDE
• Generative ODE
• PODE yields the same marginal distributions as SDE.
• It can be alseo regarded as a continuous-time flow > exact likelihood computation!
• Fast sampling, smooth interpolation!!

 

 

Controllable generation

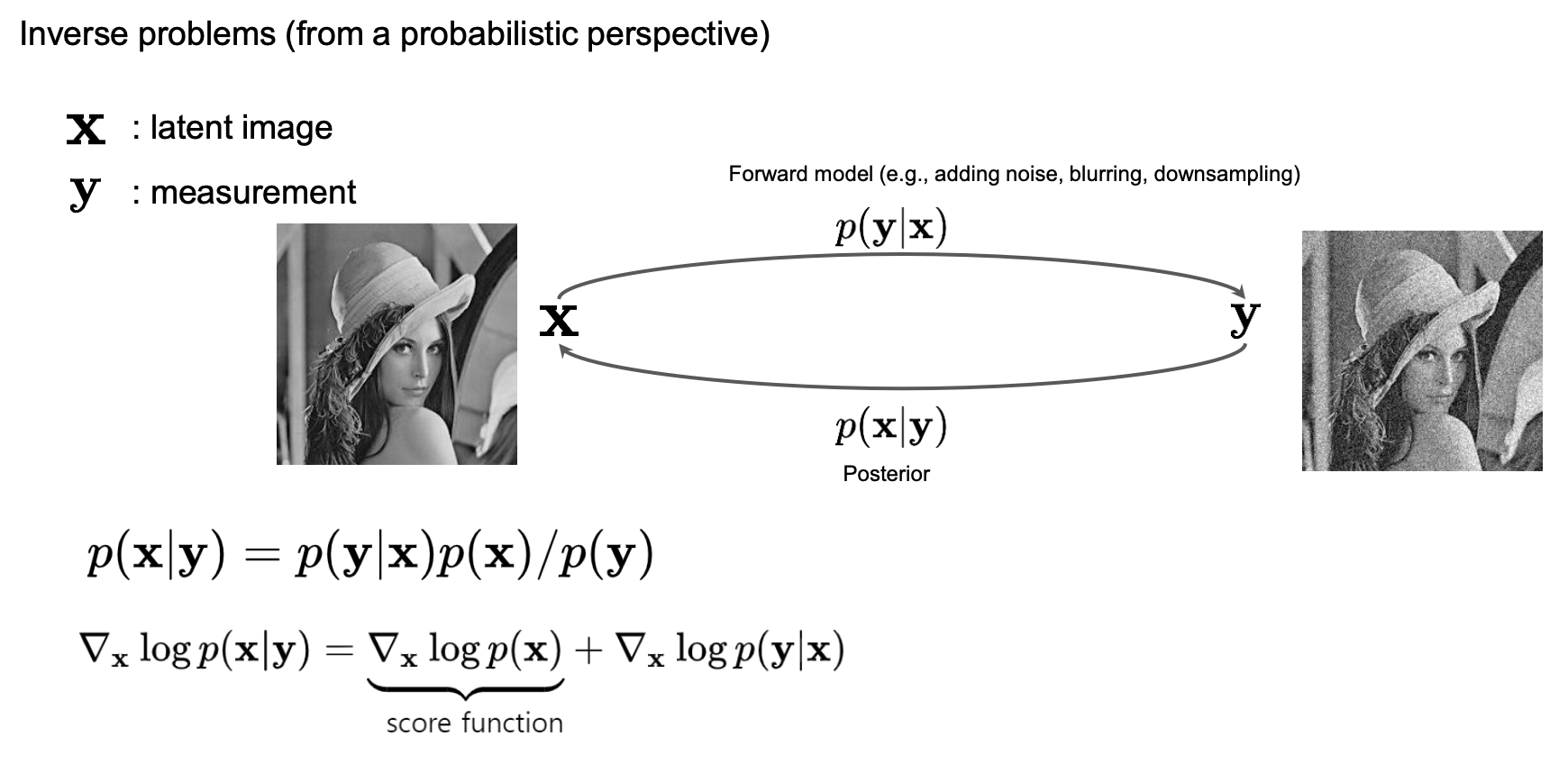
Controllable generation

 

 

 

Controllable generation

Conditional synthesis using unconditional model!

 

 

 

Classifier guidance

Classifier guidance

 

 

 

Classifier-free guidance

Classifier-free guidance

 

 

• During training, drop out the class label.
• During sampling, mix the conditional and unconditional scores to obtain the classifier gradient.

 

 

Blur diffusion

• From a SDE perspective, the generative process of diffusion models can be a reverse-time SDE of various forward stochastic processes

 

• Can we find the better forward process (and thus the generative process) tailored to a certain data modality of interes (e.g. image)?

 

 

Generate images by progressive deblurring

 

 

 

Generalized diffusion in the rotated coordinate system

 

 

 

Blur diffusion

 

 

 

Blur diffusion

 

 

 

Blur diffusion

 

 

 

Inductive bias matters!!

 

 

 

Other forward processes

Cold Diffusion: Inverting Arbitrary Image Transforms Without Noise

 

 

 

Conclusion

• Diffusion models can be viewed as the discretization of SDEs.
• DPMs and SBMs (Song & Ermon) are the discretizations of VP and VE SDEs.
• Other forward processes can also be considered (e.g. blur).

 

 

Q&A

 

 

 

 

 

 

긴 글 읽어주셔서 감사합니다 🤓